Having hit a bit of a wall trying to prove that a maximal cyclotomic matrix necessarily squares to 4I, I’ve been exploring related questions instead. For instance, it only took a couple of tweaks to my code to search for matrices that square to 3I instead of 4I; there turn out to be only finitely many, which isn’t particularly interesting. However, one of them is an 8 vertex cube which I recognised as ‘half’ the maximal cyclotomic graph S16.
This got me thinking about the properties of graphs obtained by stitching together two graphs, and lead to an interesting construction. If M squares to nI, then by taking a second copy of its graph, negating and joining each vertex in the original to the corresponding one in the copy, you get a new matrix which squares to (n+1)I.
By iterating this process, many of the maximal cyclotomic graphs can be recovered; and since there are infinite families of maximal cyclotomic graphs, I can demonstrate infinitely many non-trivial integer matrices with all eigenvales of absolute value sqrt(n) for any integer n≥5 too.
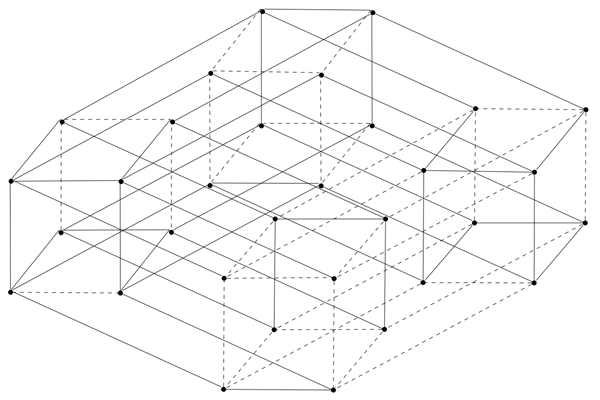
A particularly nice example is the family of signed n-hypercubes generated by running this procedure on the ‘1-cyclotomic’ graph consisting of just a line. The picture at the top of this post is of the 5th step, and I’ve put together an animation illustrating its construction:
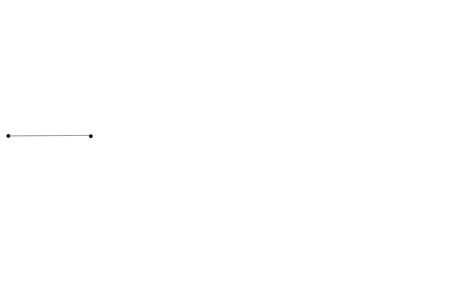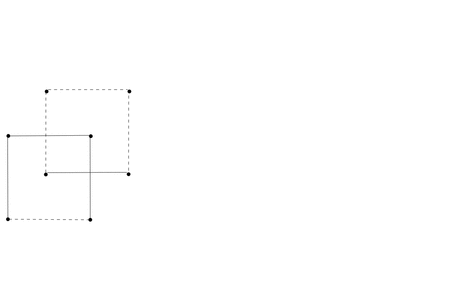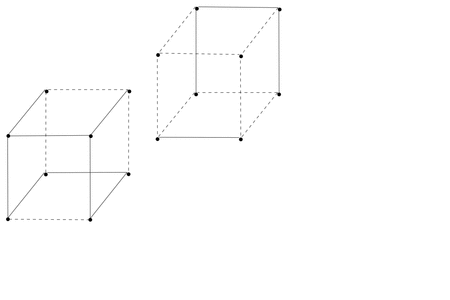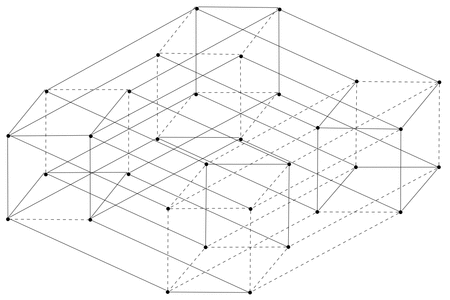
No mathematical reason to stop at 5, it just gets harder and harder to draw these things!