In this post, we describe the results of a search for all possible subgraphs consisting of two adjacent vertices a,b and all of their neighbours in G.
The route
Suppose there exists a Conway-99 graph G, that is, an SRG(99,14,1,2). Let a and b be vertices of G such that a and b are neighbours. Then:
- a has 14 neighbours, one of which is b
- b has 14 neighbours, one of which is a
- By λ = 1, precisely one of these neighbours is a mutual neighbour of both a and b
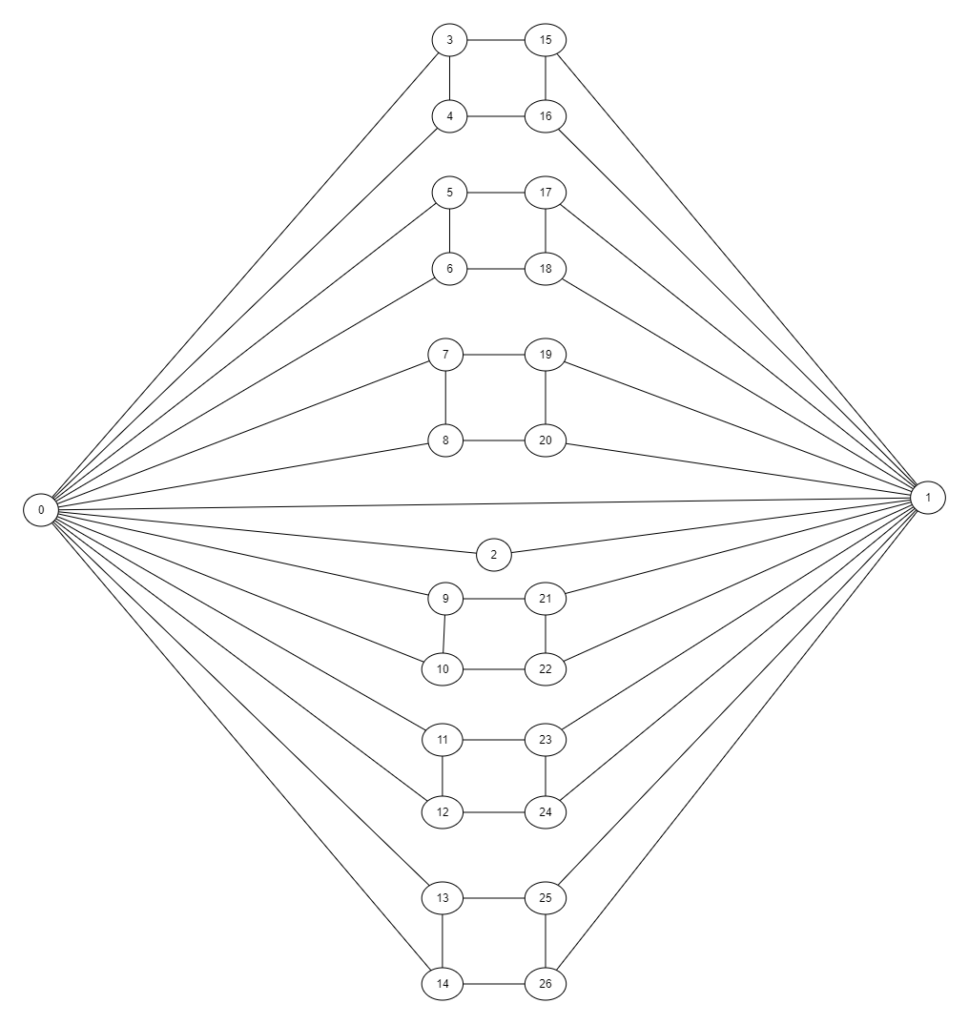
Thus the graph G’ on a,b and their neighbours consists of 27 vertices (a, b, their mutual neighbour, 12 neighbours of a but not b, and 12 neighbours of b but not a). For convenience, we fix a numbering:
- a is vertex 0
- b is vertex 1
- Their mutual neighbour is vertex 2
- The remaining neighbours of vertex a are vertices 3 through 14
- The remaining neighbours of vertex b are vertices 15 through 26
Moreover, we introduce these vertices sequentially using the ‘fanblade’ structures centred at vertices 0 and 1:
- For i,j in 1…14 we have i,j adjacent iff j = i + 1 and i is odd (as in the diagram above)
- For i,j in 15…26 we have i,j adjacent iff j = i + 1 and i is odd
- (The seventh blade for vertex 1 consists of vertices 0 and 2)
Finally, we note that each of the vertices i = 15…26 is not adjacent to vertex 0, thus (by μ = 2) there must be two mutual neighbours of 0,i in G. But as all neighbours of 0 are in G’, namely vertices 1…14, we know that each vertex i = 15…26 is adjacent to precisely 2 of the vertices 1…14.
- By assumption, vertex 1 is adjacent to vertex i
- Hence vertex 2 is not adjacent to vertex i (else 0 and i and are mutual neighbours of adjacent vertices 1 and 2, which violates λ = 1)
- So for each i = 15…26 there is a unique j in 3…14 such that i and j are neighbours.
- For the first such i=15, all choices of j give equivalent graphs on vertices 0…15. Wlog, we set j=3.
Our task then essentially reduces to determining j for each i=16…26, whilst satisfying all our other conditions.
The code
I have produced an assortment of python functions for working efficiently with strongly regular graphs, defaulting to the Conway 99-graph but (hopefully) valid for generic parameters; a public github repository is here. Included is a notebook working through this search; you can view it here if you just want the results without having to run the code yourself.
The rest of this section sketches out some of the challenges in working with srgs, particularly with regard to growing valid supergraphs from a given starting set.
‘Growing’ subgraphs
Adding vertices
As discussed in the previous post, we could in principle work our way from any subgraph G’ to G by considering all possible ways to add a vertex v’ to G’, and discarding those which can be identified as breaching a known subgraph property.
In practice we can terminate even sooner. Consider our starting subgraph N(0) on vertices 0…15. We know that vertex 0 is ‘saturated’ in that all of its neighbours are already present. So any proposed addition of vertex 16 which sets the edge (0,16) is doomed to failure; we should recognise this once rather than try all of the 32,768 possible combinations of (1,16), (2,16), (3,16) …, (15,16).
Matrix representation
Thus far we’ve described everything purely in graph-theoretic terms. However, graphs can be awkward to work with as a data structure; under the hood, we will instead use two dimensional arrays for the corresponding adjacency matrix of a graph.
Usually, this is a matrix of 0s and 1s where the (i,j)th entry is 1 if and only if vertices i and j are adjacent. (Thus when we say the adjacency matrix, we actually mean an adjacency matrix – for an unlabelled graph each choice of vertex numbering will give different – but equivalent – representatives. For this search, however, we have already prescribed a particular labelling.)
However, in the code we’ll extend this to a template form which also allows (i,j) to take the value 2, to indicate an unspecified edge and thus a collection of graphs sharing some common edges and non-edges.
A round of growing
Thus, given a set S of potential n-vertex subgraphs of G, we can grow to the set of potential (n+1)-vertex subgraphs as follows.
For each g in S:
- Form an (n+1) by (n+1) all-twos matrix a’.
- Set values a[0,0] through a[n-1,n-1] using the adjacency structure on vertices 0…n-1 given by g.
- Set the diagonal entry a'[n,n] = 0 (as the new vertex n cannot be a neighbour of itself).
- For any required edge between vertex n and some vertex i of g, set a'[i,n] and a'[n,i] = 1.
- For any required non-edge between vertex n and some vertex i of g, set a'[i,n] and a'[n,i] = 0.
- Add a’ to the template list.
Then, whilst the template list is not empty:
- Remove any a’ from the template list.
- Identify the lowest indices i,j such that a'[i,j]=2.
- Construct new arrays a0 and a1, by first copying a’ but then setting a0[i,j]=a0[j,i]=0 and a1[i,j]=a1[j,i]=1
- If a0 is a purely 0,1 array then check whether the corresponding graph violates any of the subgraph properties described in the previous post. If not, add it to the solution list.
- Otherwise, a0 is a template. However, we may already be able to rule it out, if the edges and non-edges specified thus far already specify an invalid feature (for example a vertex of degree 15, or a second mutual neighbour of vertices known to be adjacent). If no such features exist, add a0 to the template list.
- Perform the previous two steps for a1 in the same way (if an adjacency matrix, add to solution list if valid; if a template, add to template list if not already invalid).
This process necessarily terminates. If the solution list is empty, we have proven that G cannot have any g from S as a subgraph. Conversely, if the solution list S’ is non-empty, we can treat this as a new S and repeat the procedure.
If we knew that at least one of the g in S was a necessary subgraph of G, then if S’ is empty we know that G does not exist. If S’ is nonempty, we now know that at least one of the g’ in S’ is a necessary subgraph of G. Unfortunately, there may be a huge number of these!
Reducing subgraphs
Fortunately, many of them will turn out to be equivalent, as we can take alternative routes to the same (abstract) graph. For example, we argued at the start that attaching vertex 15 to any of j = 3 through 14 was equivalent, so we might as well specify that j it be vertex 3. If we hadn’t done that, we would have obtained 12 valid solutions, one for each choice of j. Having done so, our specification of vertex 16 as the mutual neighbour of vertices 1 and 15 yields 11 solutions, but these only fall into two equivalence classes.
Thus we need to be able to reduce the solution list modulo isomorphism. For the mathematical part I rely upon Nauty, via the orthogonal array package; this documentation (implicitly) describes how to compare a single pair of matrices for equivalence by comparing if they have the same normal form.
It’s easy enough to wrap this comparison up in a function on a pair of arrays. Then the solution list can be reduced by building up a representative list, adding each entry of the solution list only if it is inequivalent to all representatives added so far.
However, this soon turns out to be prohibitively expensive to compute (even with early abort when a match is found), due to the need to put both the representative and the candidate in normal form each time. It is better, therefore, to keep the normal forms along with the representatives, then normalise each candidate once and test for equality to any of the representative normal forms. Since we’re now testing equality, we can go faster by handling this as a dictionary lookup rather than sequentially working through a list… except numpy arrays are mutable and thus can’t be used as keys. Thus I took the questionable choice of converting the normalised array to a full tuple of its entries to get something hashable, likely losing all sorts of representational efficiency: a classic time/memory trade-off that has made the reduction pass negligble compared to the proceeding growing step, but will eventually cause problems!
Validity Testing
One final area where refinement proved necessary was in checking adjacency matrices or templates for invalid features. Given the size of the graphs I was able to work with, the eigenvalue constraints never came into play, so all that is implemented in the code is checks for vertices with excessive degree, adjacent vertices with more than one mutual neighbour, or non-adjacent vertices with more than two mutual neighbours.
As with equivalence testing, it’s pretty easy to write functions that compute the numbers of common neighbours, but when comparing in bulk there is simply too much repeated or otherwise unnecessary work: when you add a vertex to a valid graph, there are only a few places where it can become invalid; and as soon as you find one invalid vertex pair there’s no need to continue testing others. Thus in the code you can find _with_subgraph_mutuals versions of various functions, which again trade off some memory to avoid recomputing known (or more easily derived) values.
The Results
With these various improvements, it takes only a few seconds to recover the possible 27-vertex graphs on 0,1 and their neighbours.
There turn out to be only eleven possibilities. The first of these proceeds in the obvious way, matching 16 to 4, 17 to 5 and so on for this pleasing (after some artistic re-arrangement in yEd!) graph:
The others are more complicated; the notebook describes the differences to this baseline. We can also see that there are no edges in common to all 11; that is, our initial choices did not propagate further and we require further assumptions to force a particular subset of the solutions.
Searching further
Unfortunately, things get much worse from here. The github repo contains two ‘full search’ notebooks. The first proceeds as with our route, trying to introduce neighbours of vertex 2; this will climb to nearly 3 million 33-vertex graphs which it is unable to reduce. The second hands control over edge requirements to a ‘greedy’ version of the growing algorithm, which identifies the vertex closest to being saturated and attempts to add neighbours of that (in the hopes of reaching impossible features sooner). Tiebreaking on label, this therefore favours vertex 3 over vertex 2 but grinds to a halt sooner, at 31 vertices.
I also attempted a sampling rather than exhaustive search: this throws away all but a tiny portion of the results each round in the hope of finding a route through by chance. Unsurprisingly, this has not yielded anything, although the vertex counts attained can be decent.
Finally, it’s natural to ask for the graph consisting of two non-neighbours and their respective neighbours. This sounds like a very minor tweak on what we’ve done here: we add vertex 15 a first non-neighbour of 0, then proceed to saturate it instead of vertex 1. But this too falls victim to acombinatorial explosion of possibilities – whilst it has not yet outright crashed, I expect days of cputime to complete it.
So, for now, I offer this up for others to consider. Perhaps these 11 graphs contain enough information for a mathematical argument rather than trying to push on computationally; or perhaps some of the code I’ve written will be helpful. But if not, it was enjoyable playing around with some ‘proper’ maths for a while, and to overcome the series of programming puzzles presented by each of the search, reduction and validity checking bottlenecks.
]]>